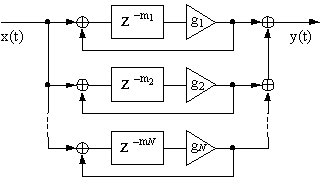
���o�[�u�͎��R�ȉ����̌��ʂł���B ���������̋N���镔���Ŕ�������ƁA�����̋ߐڂ���G�R�[�ɂ���ċ��������B �����̃G�R�[�͉��������̔��˖ʂŒ��˕Ԃ邱�Ƃɂ���ċN����B �l�H�I�ȃ��o�[�u�E�A���S���Y���Ƃ́A���܂��܂Ȍv�Z�ʂ�K�v�Ƃ����X�̎�@��p���Ă����̃G�R�[���Č����悤�Ƃ�����̂ł���B
���̏͂͐l�H�I�ȃ��o�[�u�E�A���S���Y���̊T�v�ƂȂ��Ă���B 2.1�߂ł͐l�H�I�ȃ��o�[�u�̃f�U�C���Ɋւ����̎�v�ȃA�v���[�`���Љ�A ������2.2�`2.4�߂ł͎��ۂ̕����̉��������ɂ��ĊT������B �c��̐��ł͍ŏI�I�ɐ��^�C�v�̃��o�[�u�E�A���S���Y�����������ƂɂȂ邾�낤�B
�l�H�I�ȃ��o�[�u�͈قȂ��̃A�v���[�`�ɂ���ē�����B �ŏ��̈�͕����I�A�v���[�`�ł���A���ۂ̕����̐��m�ȃ��o�[�u��l�H�I�ɍČ����悤�Ƃ�����̂ł���B ���̂悤�ȏڍׂ��邽�߂ɁA�ʏ�A���o�[�u���܂ސM���͕����̃C���p���X�����ƃ\�[�X�M������ݍ��݉��Z���邱�Ƃɂ���ē�����B �C���p���X�����͕������璼�ڋL�^���邩�A���z�I�ȕ����̊I���f����p���邱�Ƃœ�����B ��҂̃P�[�X�ł́A�����̊I�ȓ����i�傫����ǂ̍ގ��Ȃǁj���C���p���X�����̌W�����v�Z���邽�߂ɗ��p�����B
���̃A�v���[�`�̓\�[�X�ƒ�����̈ʒu���^������ΐ��m�ȕ\�����\�ł�����̂́A ���A���^�C���E�o�[�`�����E���A���e�B��Q�[���Ȃǂ̗p�r�ɂ����Ă͏_��ƌ����̖ʂł����Ώ\���ł͂Ȃ��B ���Ƃ��A3�b�Ԃ̃I�[�f�B�I�M����2�b�Ԃ̕����̃C���p���X�����i44.1kHz�ŃT���v�����O�j�����ԗ̈�ŏ�ݍ��݉��Z����ɂ́A �����悻120����̏�Z��220,500��̉��Z���K�v�ƂȂ�B �����Ȏ��g���̈�ɂ��Ă̏�ݍ��݉��Z�ł�220,500��̕��f���̏�Z���K�v�ƂȂ��A�ϊ�����ыt�ϊ���Ƃ̃I�[�o�[�w�b�h�������B
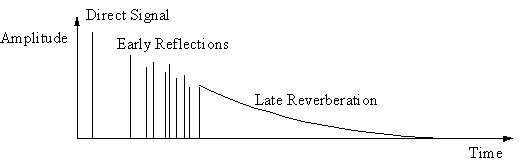
���̃A�v���[�`�͒m�o�I�A�v���[�`�ƌĂ�A ���R�̃��o�[�u�Ɓu�m�o�I�ɋ�ʂł��Ȃ��v�l�H�I�ȃ��o�[�u�E�A���S���Y���ݏo�����Ƃ�����̂ł���B �����̃A���S���Y���̖ړI�͎��R�̃��o�[�u�̖ڗ������������Č����邱�Ƃł���B ���̃A�v���[�`�͕����I�ȃA�v���[�`����ʂɂ͂邩�Ɍ����I�ŁA ���z�I�ɂ́A���������A���S���Y�������S�Ƀp�����[�^�����邱�Ƃ��ł��邩������Ȃ��B ���̘_���ł͂�����̃A�v���[�`�ɒ��ڂ���B
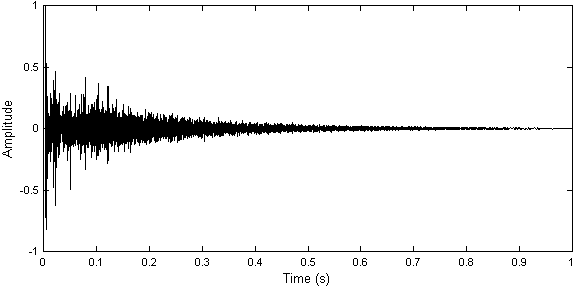
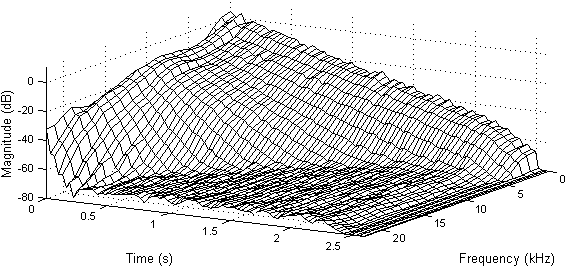
�����n�l���[�e������i�E�B�X�R���V���B�}�f�B�\���j�̃C���p���X������Fig. 2.1�Ɏ����B ����Ɍ�����悤�ɁA�g�`�̍ŏ��̕����i0�`150 ms�j�͗��U�I�ȃs�[�N�ō\������Ă���A �㔼�����͂��ώ��łقƂ�ǎw�����I�Ɍ������Ă���B ���̃C���p���X�����́AFig. 2.2�Ŏ����悤�ɎO�̕ʌ̕����ɕ����ă��f�������邱�Ƃ��ł���B ���f���ɂ��A�C���p���X�����͒��ڂ̐M���ɉ����āu�A�[���[�E���t���N�V�����v�ƌĂ�闣�U�I�ȃG�R�[ �i�ǂ⏰�A�V��ɗR������j�A�����āu���C�g�E���o�[�u���[�V�����v����\�������B

����͐l�H�I�ȃ��o�[�u�E�A���S���Y������̕����ɕ������邱�Ƃ������Ă���B �ŏ��̕����Ŏ��ۂ̃C���p���X�����Ɉ�v����L���̗��U�I�ȃG�R�[�����A ���̕����Ŏw�����I�Ɍ������鍂���G�R�[�̖��x������Ηǂ��̂ł���B
��ʓI�ɁA�A�[���[�E���t���N�V�����̓V�~�����[�g���ꂽ�����̊I���f������v�Z�����B �ł������p�����Ă���̂́u�\�[�X�E�C���[�W�@�v�Ɓu���C�E�g���[�V���O�@�v�ł���B �����͑o���Ƃ������`�B���iHRTF�j�Ƒg�ݍ��킹����B �����̋Z�p�ɂ��Ă̋c�_�͂��̘_���͈̔͂��z����B �������Ȃ���A�D�ꂽ�T�v��[10]��[51]�Ɍ�����͂��ł���B 2.3�߂�2.4�߂ł͂������Ɏ��ۂ̕����ɂ����郌�C�g�E���o�[�u���[�V�����̓����ɂ��ĊT������B ���C�g�E���o�[�u���[�V�����̃��f�����ɂ��Ă�2.5�`2.7�߂ŏڂ����c�_���邱�ƂƂ���B
�����͂������̃��o�[�u�E�^�C���iRT�j�ɂ���ē����Â����A ���̊T�O��1900�N�ASabine [33]�̎��������ɂ�������I�Ȍ����ɂ���Ċm�����ꂽ�B ���o�[�u�̌������Ԃ͕����̗e�ςɔ�Ⴕ�A�ǂ⏰�A�V��̋z���ʂɔ���Ⴗ��B
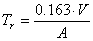
Tr�����o�[�u��60dB��������̂ɂ����鎞�ԁis�j�ł���Ƃ���Ƃ��A V�͕����̗e�ρim3�j�ł���AA�͕����̑S�z���ł���B �����̋z���͎��g���ˑ��ł��邽�߁A�����̃��o�[�u�E�^�C�����܂����g���ˑ��ł���B �Ⴆ�A�����������g���z�����鑽�E���̍ގ��łł����ǂ��܂ޏꍇ�ART�͎��g�����オ��ɂ�Ă��Z���Ȃ�B
RT�𑪒肷��ׂ��ASchroeder [40]�͕����̃G�l���M�[�E�f�B�P�C�E�J�[�u�iEDC�j�邽�߂� �����̃C���p���X������ϕ����邱�Ƃ��Ă����B
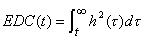
������h(t)�͕����̃C���p���X�����ł���A����̎��g���ш��EDC�邽�߂Ƀt�B���^�������邱�Ƃ��ł���B
Jot [17]��Griesinger [14] �̓��o�[�u�̎��g���ˑ��������o�����₷�����邽�߁A���̊T�O���g�������B Jot�̓G�l���M�[�E�f�B�P�C�E�����[�t��������EDR�it,w�j�ƌĂ��EDC�̕ό`���Ă����B EDR��3D�v���b�g�Ƀ��o�[�u�E�f�B�P�C�����ԂƎ��g���̊��Ƃ��ĕ\���B ������v�Z���邽�߁A�C���p���X�������̎��g���ш�ɕ������ASchroeder�̐ϕ����v�Z���A���ʂ�3D�ǖʂɃv���b�g����B ���Ƃ��āA�T�^�I�ȃz�[����EDR��Fig. 2.3�Ɏ����B �C���p���X�����͒���g�ɂ����Ă͂������ƌ������邱�Ƃ�������B �������Ȃ���A�ǂ�����g��荂���g���z�����邽�߁A�����g�ɂ����郊�o�[�u�E�^�C���͔��ɒZ���Ȃ��Ă���B
�����͐U���̊�`�ɂ���ē����t�����A����͕����ɂ���Ď��R�ɑ������ꂽ���g���ł���B ���g��f�̂��Ƃł̊�`�̐�Nf�͕����̌`�� [24]�ƂقƂ�ǖ��W�ł���A�����ɂ���ė^������B
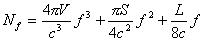
������V�͕����̗e�ρim3�j�Ac�͉����im/s�j�AS�͕ǂ̕\�ʐς̍��v�im2�j�A ������L�͕����̑S�Ă̗ł̒����̍��v�im�j�ł���B �w���c���̃��[�h�̐��Ƃ��Ē�`����郂�f���E�f���V�e�B�͎����ɂ���ĕ\�����B
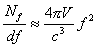
���̂悤�ɁA�����̃��f���E�f���V�e�B�͎��g���̎���ɔ�Ⴕ�đ��傷��B ���̌����ɂ��A���K�͂̃z�[���i18,100 m3��RT��1.8�b�Ƃ���j�� 1kHz�ɂ����ăw���c����5800���[�h�̎��g�����x�������ƂɂȂ�B
�������Ȃ���A�ՊE���g�����z����ƁA���[�h�͏d�Ȃ�n�߂�B ���̗ՊE���g�����z����ƁA���[�h�͑��݂Ɉ�ĂɎh���������A�A������B ����͓��v�I�Ƀ��f�����������g�����������o���B [24] [42] ���̃��f���ɂ��A���ϓI�ȊԊu���������ő���g���ɂ���ē����t�����镔���̎��g�������͎����̂悤�ɕ\�����B
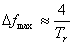
������Tr�̓��o�[�u�E�^�C���ł���B ���̓��v�I���f���͗ՊE���g������ł̂ݐ������B
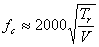 Hz
Hz
������Tr�̓��o�[�u�E�^�C���AV�͕����̗e�ςł���B
���̃��f���ɂ��A���K�͂̃z�[���i18,100 m3��RT��1.8�b�Ƃ���j��
�ՊE���g��fc = 20 Hz�̏�ɂ�����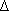 fmax
= 2.2 Hz �̕��ςŕ�����ꂽ���g���s�[�N���\��������g�������������ƂɂȂ�B
fmax
= 2.2 Hz �̕��ςŕ�����ꂽ���g���s�[�N���\��������g�������������ƂɂȂ�B
������̎�v�ȕ����̓����͎��ԗ̈�ɂ�����G�R�[�̖��x�ł���B �����̃G�R�[�E�f���V�e�B�͕b�Ԃɕ�����ɓ͂��G�R�[�̐��Ƃ��Ē�`�����B Kuttruff [24]�̓G�R�[�����Ԃ̎���ɔ�Ⴕ�đ������邱�Ƃ��������B �i���������f��������̂ɋ���p�����\�[�X�E�C���[�W�@�𗘗p�j
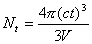
������Nt�̓G�R�[�̐��At�͎��ԁis�j�A ct�͋��̒��a�im�j�A������V�͕����̗e�ρim3�j�ł���B t�ɂ��Ĕ������邱�ƂŃG�R�[�̖��x��������B
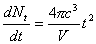
������Nt�͎���t�is�j�ȑO�ɐ�����G�R�[�̐��A c�͉��̑����im/s�j�A������V�͕����̗e�ρim3�j�ł���B
�G�R�[�E���X�|���X�����v�I�ɎU���������ɂȂ�ȍ~�̎��Ԃ́A���͐M�����Ɉˑ�����B
���̃p���X 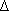 t�Ɋւ��āA
�G�R�[���d�Ȃ荇���n�߂�ȍ~�̗ՊE���Ԃ�[38]�ɂ��Ĉȉ��̂悤�ɂȂ�B
t�Ɋւ��āA
�G�R�[���d�Ȃ荇���n�߂�ȍ~�̗ՊE���Ԃ�[38]�ɂ��Ĉȉ��̂悤�ɂȂ�B
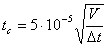
�Ⴆ�A10,000 m3�̕�����1 ms�̃C���p���X�ɂ���ċ������ꂽ�G�R�[�� 150 ms�ȍ~�ɏd�Ȃ荇���n�߂�B ���̎��Ԃ��z����ƁA���͂�ʂ̃G�R�[�����m���邱�Ƃ͂ł��Ȃ��B
�傫�ȕ����̂�����̓����͋ߐڂ�����g�����[�h����̓������x�Ō������邱�Ƃł���B ��������A�Ⴂ���g����荂�����g���̕���������������Ƃ��Ă��A �����̈�ɂ���S�Ă̎��g���͓������x�Ō�������̂ł���B �����ŗ��ӂ��ׂ��́A�悭�����镔���ɂ����Ắu���d�����v �i�������s�ȓ�̍d���ǂ̊Ԃ���������Ƃ��ɔ�����������I�ȃG�R�[�j�����邱�Ƃ��ł��Ȃ����Ƃł���B
���ۂ̕����ł̃��o�[�u�̓����ɂ��Ă͏q�ׂ��̂ŁA �l�H�I�ȃ��o�[�u�����邽�߂ɊJ�����ꂽ�ʂ̕��@�ɏœ_�Ă悤�Ǝv���B
Schroeder [38]�̓x���������ւ̋Α����Ƀf�W�^���E���o�[�u�̍쐬�����߂Ď��݂��p�C�I�j�A�ł���B �ނ��ŏ��Ɏ���������i�̓R���t�B���^�iFig. 2.4�ɐ}���j�ƌĂ�A ��������g�����t�B�[�h�o�b�N���[�v�ƒP�Ƃ̃f�B���C�E���C���ō\�������B
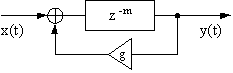
Fig. 2.5��Fig. 2.4�Ŏ��������̂Ɏ����R���t�B���^�������Ă���B ������������̐v�ł́A�����������t�B�[�h�o�b�N�o�H�ł͂Ȃ����ڌo�H�ɂ���B ���傫�Ȑv�̍\���v�f�Ƃ��č쓮���邽�߁A���̘_���̎c��̕����ł͂�����̍\���𗘗p���邱�ƂƂ���B �����ŗ��ӂ��ׂ��́A��̐v�͂ǂ���������悤�ȃC���p���X�����ݏo�����A g���q�ɂ���Ĉ�����������キ�Ȃ�Ƃ������Ƃł���B

Fig. 2.5�̃R���t�B���^��Z�ϊ��͎����ɂ���ė^������B
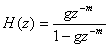
������m�̓f�B���C���i�T���v���j�Ag�͌��������ł���B
���ӂ��ׂ��́A����̂��߂ɂ�g��1�ȉ��łȂ���Ȃ�Ȃ��Ƃ������Ƃ��B
�t�B�[�h�o�b�N���[�v��������邽�тɁA����20  log10(g) dB��������B
����āA�R���t�B���^�̃��o�[�u�E�^�C���i60 dB�̌����Ƃ��Ē�`�����j�͎����ɂ���ė^������B
log10(g) dB��������B
����āA�R���t�B���^�̃��o�[�u�E�^�C���i60 dB�̌����Ƃ��Ē�`�����j�͎����ɂ���ė^������B
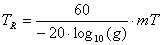
������g�͌��������Am�̓f�B���C���i�T���v���j�A ������T�̓T���v�����O�����ł���B
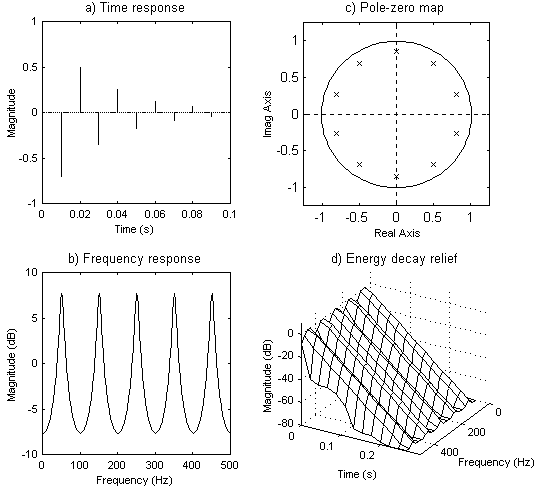
�R���t�B���^�̓�����Fig. 2.6�Ɏ����B �G�R�[�̐U���͎��Ԃ���������Ǝw�����I�Ɍ������邱�Ƃ�������B ����͎��ۂ̕����̃��o�[�u�̌㕔�����w�����I�Ɍ������邱�Ƃ���D�s���ł���B �������Ȃ���A���̓G�R�[�E�f���V�e�B���Ⴍ�A�Z���̓��͂ɑ��Ắu�тт�v���������N�����B ���̏�A�G�R�[�̖��x�͎��ۂ̕����̂悤�Ɏ��ԂƂƂ��ɑ������邱�Ƃ͂Ȃ��B
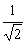 ).
).�R���t�B���^�̋ɗ�z�u�́Am�T���v���̃f�B���C�E���C���� �P�ʉ~���ɑ���m�̓��Ԋu�̋ɂ����o�����Ƃ������Ă���B �ɂ̔�����0 Hz�ƃi�C�L�X�g���g��f = fs/2 Hz�̊ԂɈʒu���A ������fs�̓T���v�����O���g���ł���B ���ꂪ�A���g�����������o�[�u�̌㕔�Ɂu�����I�ȁv���������炷m�̂͂����肵�����g���s�[�N�������R�ł���B ���g�������̃s�[�N�ɑ������鉹�F���ق�̏���������邱�Ƃ��ł��邾���Ȃ̂ŁA ���̂悤�ȉ��͋����I�Ȃ��̂Ƃ��Ēm�o�����B
�f�B���C��m���G�R�[�E�f���V�e�B�������邽�߂Ɍ��炷�ƁA ���g���̈�̃s�[�N�����Ȃ��Ȃ邽�߂Ƀ��f���E�f���V�e�B����܂錋�ʂƂȂ�B �]���āA���Z�����o�[�u�����o���ړI�ŃG�R�[�E�f���V�e�B��������ƁA ���ʓI�ɓ���̎��g���ŋ��U���鉹�ɂȂ��Ă��܂��B ���̃t�B���^�ɂ��ė��ӂ��Ă����Ȃ���Ȃ�Ȃ��Ō�̏d�v�����́A �t�B�[�h�o�b�N����g��������ƌ������x���Ȃ� �i�܂�����ɂ���ă��o�[�u�E�^�C���������Ȃ�j�Ƃ������Ƃł���B ���g���̕ϓ��̍ő�E�ŏ��l�������ł��邱�Ƃ���A ����͂�肢�������ڗ��s�[�N�������炷���ƂɂȂ�B
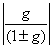
����܂ł̐v�ł̎��g�������������邽�߁A Schroeder�̓I�[���p�X�E���j�b�g�ƌĂ����̂����o�����B�����Fig. 2.7�Ɏ����B ���̃t�B���^�̓����̃t���[�_�C�A�O�����͈قȂ���̂����A �����Ŏ��������̂Ƃɂ��đo���̃t�B���^�̓����͓����ł���B
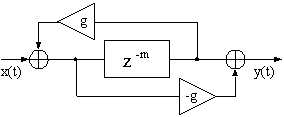
�I�[���p�X�t�B���^��Z�ϊ��͎����ɂ���ė^������B
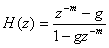
�]���ăI�[���p�X�t�B���^�̋ɂ̓R���t�B���^�Ɠ����ʒu�ł��邪�A �����t���̈ʒu�ɂ�����0���lj������B ���̐v�̎��g�������͎����ɂ���ė^������B
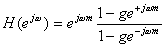
�S�Ă� �ɑ��Ď��g���������P��ł��邱�Ƃ�������B
�����
�ɑ��Ď��g���������P��ł��邱�Ƃ�������B
�����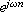 ���P�ʐU���������A
���f�����̎w�����܂�����̐U����������ł���B
���̂��Ƃ��玟���������o�����B
���P�ʐU���������A
���f�����̎w�����܂�����̐U����������ł���B
���̂��Ƃ��玟���������o�����B
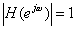
�I�[���p�X�t�B���^�̓�����Fig. 2.8�Ɏ����B ����ŕ�����悤�ɁA�t�B�[�h�t�H���[�h�o�H��p���邱�ƂŁA Schroeder�̓t���b�g�Ȏ��g�������������o�[�u�E���j�b�g��ꂽ�̂ł���B ����āA����ԐM���͋r�F���ꂸ�Ƀ��o�[�u���[�^����o�Ă���B �������Ȃ���A�ߓn�I�ȐM���ɂ��Ă̓��j�b�g�̎��g�����x���\���ɍ����Ȃ��A �܂��R���t�B���^�̉��F����������B
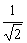 ).
).�R���t�B���^�ƃI�[���p�X�t�B���^�o�����A���� |g| = 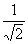 �ɂ��ē����C���p���X�����i�ŏ��̃p���X�������j�������Ƃɒ��ڂ���Ƌ����[���B
����g�����̒l�ł����Ă��A�Z���ߓn�I�ȓ��͂ɂ��Ă�
�o���̐v�̉��͎������̂ɂȂ邱�Ƃ�������B
�Z���Ԃł͑S�̂̎��g�������Ƃ܂�ňقȂ邩������Ȃ����Ƃ���A
�t�B���^�̎��g�������v���b�g�����Ĉ����̂Ɏ��ܐT�d��v����B
����Ȃ킯�ŁA���o�[�u�E�A���S���Y���̕i����]�����邽�߂ɂ����C���p���X��p����B
����͎��ԗ̈�A���g���̈�o���ɂ��Ẵ��o�[�u���[�^�̕i���ɗǂ��ڈ���^���Ă����B
�ɂ��ē����C���p���X�����i�ŏ��̃p���X�������j�������Ƃɒ��ڂ���Ƌ����[���B
����g�����̒l�ł����Ă��A�Z���ߓn�I�ȓ��͂ɂ��Ă�
�o���̐v�̉��͎������̂ɂȂ邱�Ƃ�������B
�Z���Ԃł͑S�̂̎��g�������Ƃ܂�ňقȂ邩������Ȃ����Ƃ���A
�t�B���^�̎��g�������v���b�g�����Ĉ����̂Ɏ��ܐT�d��v����B
����Ȃ킯�ŁA���o�[�u�E�A���S���Y���̕i����]�����邽�߂ɂ����C���p���X��p����B
����͎��ԗ̈�A���g���̈�o���ɂ��Ẵ��o�[�u���[�^�̕i���ɗǂ��ڈ���^���Ă����B
������̃��j�b�g�E�t�B���^��l�X�ȕ��@�őg�ݍ��킹�邱�ƂŁA ��蕡�G�ȍ\�������o�����Ƃ��ł���B ���܂��������̌��ʁA���傫�ȃG�R�[�̎��Ԗ��x�������A ��芊�炩�Ȏ��g�������������o�[�u�ݏo�����Ƃ��낤�B�s���ߓn�I�ȓ��͂ɂ��Ă����ł���B
�l�H�I�ȃ��o�[�u�̎��Ԗ��x�������邽�߁A Schroeder�̓I�[���p�X�̎��g�����������t�B���^�悤�ƁA �����̃I�[���p�X�t�B���^��ڑ������B ���̌��ʂ�Fig. 2.9�Ɏ����B

���̍\���ł́A�ŏ��̃I�[���p�X�E���j�b�g���G�R�[���A �j�i�K�ڂł͂�肢�������̃G�R�[�����A �c��̒i�K�ɂ��Ă��ȉ����l�ł���B �������Ȃ���AMoorer [27][1]���w�E�����悤�ɁA �s���ߓn�I�ȓ��͂ɂ��Ă̓��o�[�u�̕s���R�ȐF�������c���Ă���B
���j�b�g�E�R���t�B���^���������̎��g���s�[�N�����Ƃ͂����A �������̃R���t�B���^�����ɑg�ݍ��킹�����̂́A �قڎ��ۂ̕����̎��g�������̂悤�ȑS�̂̎��g�����������t�B���^�������B ���̐v�ł́A�e���j�b�g�E�R���t�B���^�͈قȂ�f�B���C���������A �^����ꂽ�ʒu�ȊO�̎��g���s�[�N�������Ƃ��������B ����R���t�B���^�v�̗��Fig. 2.10�Ɏ����B
�ǂ����ʂ邽�߁A�e���j�b�g�E�R���t�B���^�͓K�ɏd�݂Â����Ă��Ȃ���Ȃ�Ȃ��B �����āA�S�Ẵt�B���^�̃��o�[�u�E�^�C��������łȂ���Ȃ�Ȃ��B ���̂��߂ɂ́A( 2.11 )����ʉ����A�����ɂ���ė���gp��I�肷�邱�Ƃ��ł���B
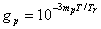 p = 1, 2,�,N
p = 1, 2,�,N
������N�̓R���t�B���^�̐��ł���B
Schroeder�́A�ő�ƍŏ��̔䗦���1.5�Ƃ���悤�Ƀf�B���C����I�肷�邱�Ƃ��Ă����B ���̕���R���t�B���^�v�́u�t�B�[�h�o�b�N�E�f�B���C�E�l�b�g���[�N�iFDN)�v�v�ɂȂ��邱�ƂɂȂ�B ����ɂ��Ă�chapter 3�Ő[���@�艺���ċc�_����B
���o�[�u�̐F���ŏ����ɂ��Ȃ���ǂ��G�R�[�E�f���V�e�B�邽�߁A Schroeder�̓R���t�B���^�i����ڑ��j�ƃI�[���p�X�t�B���^�i����ڑ��j������u���A Fig. 2.11�Ɏ������o�[�u���[�^���Ă����B �R���t�B���^�ɂ�30�`45 ms�ɕ��z����f�B���C���A��̃I�[���p�X�t�B���^�ɂ� ��̂��Z���f�B���C���i5, 1.7 ms�j��I�肵���B �R���t�B���^�̌���������( 2.16 )�ɂ���đI�肳��A�I�[���p�X�̗����͗����Ƃ�0.7�Ƃ����B ���̐v�ł́A�R���t�B���^���������o�[�u�E�f�B���C��^���A ��荂���x�ȃ��o�[�u����邽�߁A�I�[���p�X�t�B���^�������̃G�R�[��������B �������Ȃ���A�܂��\���ɍ����G�R�[�E�f���V�e�B��ł��Ȃ����߁A���̐v�͐l�H�I�ȉ�������B �܂��A���o�[�u�̌㕔�ɕ������鋤������g�������݂���B
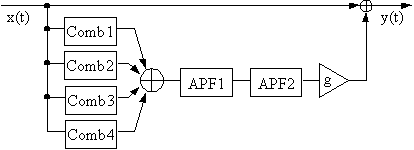
�܂��APiirilä [29]�̓R���t�B���^�ƃI�[���p�X�t�B���^�̑g�ݍ��킹�� ���ݏo���ꂽ��w�����I�Ɍ������郊�o�[�u�ɗp���邱�Ƃ��Ă����B �ނ͋����[�����y�I�ȃG�t�F�N�g�ƃ��o�[�u�̂��������X�s�[�`�̋������������邽�߂ɁA �������̈قȂ郊�o�[�u�̃G���x���[�v�ݏo�����Ƃ��ł����B
���̐߂ł͍��܂ł��̘_���œ������Ă��Ȃ�����������^�C�v�� ���o�[�u���[�^�ɂ��ċc�_����B �������A�����̂����̊���ɂ��ẮA�t�B�[�h�o�b�N�E�f�B���C�E�l�b�g���[�N�ɂ���� ��肢���������R�������I�ȃ��o�[�u���[�^�����o���悤�ɑg�ݍ��킹�邱�Ƃ��e�Ղɂł��邱�Ƃ��낤�B
��莩�R�ȉ������郊�o�[�u�E�l�b�g���[�N�邽�߂ɂ́A ���ۂ̕����ŋN����ł��낤�悤�ɁA�G�R�[�̐ςݏd�˂����o���悤�� ���j�b�g�E�t�B���^��g�ݍ��킹�邱�Ƃ͖]�܂������낤�B Vercoe [49]�ɂ���Ē�Ă���A���Bill Gardner [5]��William G. Gardner [7]�ɂ���� ���p���ꂽ�ЂƂ̉�@�́A����q�I�[���p�X�t�B���^��p���邱�Ƃł������B ���̃_�C�A�O�����ł́A���j�b�g�E�I�[���p�X�t�B���^�̃f�B���C���C�����A �`�B��G(z)�������̃I�[���p�X�t�B���^�ɂ���đ�ւ��Ă���B
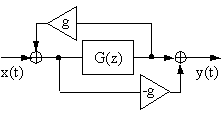
G(z)���I�[���p�X�̎��g�����������Ƃ��A ���ʂƂ��Ă��̃t�B���^���܂��I�[���p�X�̉����������ƂɂȂ�B ����̓V�X�e���̑S�̓I�Ȉ��萫�Ǝ��g��������ۏ��Ȃ���A ������[�x�̓���q�I�[���p�X�t�B���^�̎g�p���\�Ƃ���B �������AGardner�͂��̐v�ł͂܂������F�Â����ꂽ������^���邱�Ƃ������B �������Ĕނ̓V�X�e���ɃO���[�o���ȃt�B�[�h�o�b�N�o�H�i����|g| < 1 �����j�������邱�Ƃ��Ă����B ���̐V���ȕt�������ɂ��A�����炭�t�B�[�h�o�b�N���[�v�ɂ���Ă����炳�ꂽ �G�R�[�E�f���V�e�B�̑�������A���ʂƂ��ă��o�[�u�͔��Ɋ��炩�ɂȂ����B
Dattorro [3]��Griesinger�̌����ɒ��z�A �v���[�g�E���o�[�u���[�^�̃t���[�_�C�A�O�����iFig. 2.13�j���������B
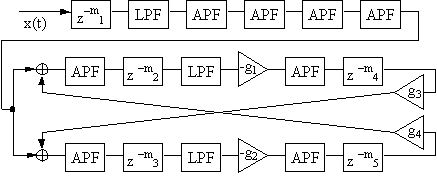
���̃��o�[�u���[�^�̍ŏ��̕����̓v���f�B���C�E���j�b�g�A���[�p�X�t�B���^�A �����ăf�B�t���[�U�Ƃ��ė��p�����4�̃I�[���p�X�t�B���^�ɂ���č\�������B �f�B�t���[�U�͓����Ă���M���̑��֊W���ɉ����A ���o�[�u���[�^�̑��̕����ɓ���邽�߂̏��������邽�߂ɗp������B Dattorro���u�^���N�v�ƌĂԑ��̕����́A���݂Ƀt�B�[�h�o�b�N������̌o�H�ɂ���č\�������B ���ꂼ��̌o�H��2�̃I�[���p�X�t�B���^�A2�̃f�B���C���C���A�����ă��[�p�X�t�B���^���琬��B �^���N�̃f�B���C���C���ƃI�[���p�X�E���j�b�g��������o�����o�͂��ɍ��v����i�l�X�ȏd�݂Łj���ƂŁA ���̃��o�[�u���[�^�̏o�͂����o�����Ƃ��ł���B 4.3.1�߂ŋc�_����悤�ɁA�^���N�̃I�[���p�X�t�B���^�͂����炳��郊�o�[�u�����炩�ɂ��邽�߂ɒ������꓾��B
���̏͂̏��߂Ɍ��y�����悤�ɁA���ۂ̕����̃C���p���X������ �M������ݍ��݂��ă��o�[�u�����o�����@�́A �������̗p�r�ɂ͏_��ƌ������\���ł͂Ȃ��B �������A���i���ȃ��o�[�u���K�v�ȂƂ��A����͉��������B ���Ƃ��ASonic Foundry�́uAcoustic Modeler�vDirectX�v���O�C���̂悤�� �s�̃\�t�g�E�F�A�́A���A���ȃ��o�[�u�����o�����߁A ���[�U�ɂ�����I�[�f�B�I�f�ނ����ۂ̕����̃C���p���X�����ŏ�ݍ��݂��邱�Ƃ����e���Ă���B ���ԗ̈��ݍ��݂��c��ȏ����\�͂�v�����邽�߁A �u���b�N��ݍ��� [9]��}���`���[�g�E�t�B���^�����O [48]�̂悤�Ȃ������̕��@���A �����v���⏈���̓��o�͂̒x��������������ׂ��J�����ꂽ�B
��ݍ��݂���Ɏ��ۂ̕����̃C���p���X�����ɂ���čs����킯�ł͂Ȃ����Ƃɗ��ӂ��ׂ��ł���B ���͂��w�����I�Ɍ�������K�E�X���F�G���ŏ�ݍ��݂���Ɨǂ����ʂ������邱�Ƃ��m���Ă��� [26]�B
���q���o�[�u���܂���ݍ��݃x�[�X�̃��o�[�u�̓T�^�ł���B �����q�����iAGS�j�ƌĂ��Z�p�ɂ���Đ�������鉹�́u���q�v�� ���͂���ݍ��݂��邱�ƂŁA���ꂼ��̗��q���瓱���ꂽ���z�I�ȁu���ˉ��v���₪�ē��͐M����s�N���ɂ���B �����炳��郊�o�[�u�̓��F�͗��q�̃X�y�N�g���ɂ���Č��肳��A ����͗��q�̌p�����ԁA�G���x���[�v�A�����Ĕg�`�Ɉˑ�����B ���q���o�[�u�ɂ��Ă̂���Ȃ�ڍׂ�[30]�Ɍ�����B
��莩�R�ȉ��̂��郊�o�[�u�����o�����߂ɁA ���o�[�u���̃X�g���[���ɕ������邱�Ƃ��ł��A �����Ŋe�X�g���[���͕����̓���̗̈���V�~�����[�g���邽�߂ɍ��킹����B ���̖ړI�ɂ͈ȑO�Ɍ��y����������t�B���^�𗘗p���邱�Ƃ��ł��A ���ꂼ��̃t�B���^�̓��o�[�u���[�^�̈قȂ�o�͂Ɋ��蓖�Ă���B �܂������́A�����`�B���iHRTF�j���f���̂悤�ȑ��̎�@��p���邱�ƂŁA �X�e���I�̈�ɂ����鉼�z�I�Ȉʒu���e�t�B���^�ɗ^����悤�����Ƀ~�b�N�X�����B
�Ⴆ��Stautner��Puckette [47]�́A���݂Ƀl�b�g���[�N�����ꂽ4�̃R���t�B���^ �i�E�A���A�����A��̃X�s�[�J�ɑΉ�����j���琬�郊�o�[�u���[�^��v�����B ���̓��L�̐v�ł́A�ŏ��ɍ��̃X�s�[�J���畷�������M���� ���ɐ��ʁA�ォ�畷�����A�Ō�ɂ͉E�̃X�s�[�J���畷������B
�}���`���[�g�E�A���S���Y���͐M����l�X�Ȏ��g���ш�ɕ�������B ���ꂼ��̃R���t�B���^���قȂ���g���ш����������悤�� �I�[���p�X�t�B���^�̃o���N�ƃR���t�B���^�̃o���N��g�ݍ��킹�邱�ƂŁA ������g���ш�̃��o�[�u�E�^�C���͑Ή�����R���t�B���^�̃t�B�[�h�o�b�N���������邱�ƂŒ�߂���B ���̍\���ł́A���̑ш敝�ɂ���Ă��ꂼ��̑ш�ɈقȂ�T���v�����[�g��p���邱�Ƃ��\�ł��� [50]�B
�f�W�^�����g�H�͊y��̕������f���ɍL���p�����Ă���B Julius O. Smith [45]�͐l�H�I�ȃ��o�[�u�̍쐬�ɉt�f�W�^�����g�H�l�b�g���[�N�iDWN�j ��p���邱�Ƃ��Ă����B ���g�H�͓�̐����̕����ɔg���L����o�����̃f�B���C���C���ł���B �g�����g�H�̏I�[�ɓ��B����ƁA�n�_�̕��ɔ��˂����B �����̓��g�H���t�l�b�g���[�N�ő��݂ɐڑ������Ƃ��A �����ŋN���锽�����V�~�����[�g����A��˂Ƀ��o�[�u���[�^�����o�����B �܂��A���[�p�X�t�B���^���t�l�b�g���[�N�̌��^�ɉ����邱�ƂŁA ���g���ˑ��̃��o�[�u�E�^�C����������B �f�W�^�����g�H�l�b�g���[�N�ɂ��Ă��ڂ�����Chapter 3�Ŏ����B
�܂����g�H�́A2D���b�V��[35] [36]���肢���������G��3D���b�V��[34]���`������ ���\�������ꂽ���@�Őڑ������B �f�W�^�����g�H�������b�V���́A���ꂼ��̓����ɉ����Ĕz�u���ꂽ �f�W�^�����g�H�̔z��ł���A��_�ő��݂ɘA�����Ă���B ���Ƃ��A�����炳���3D��Ԃ̃��b�V���� �e�m�[�h�����̗אڂ���6�ƃ��j�b�g�E�f�B���C�ɂ���Đڑ����ꂽ�����i�q�ł���B ���̍\���̖��_�̈�́A�g�̕��U�������ˑ��ł��邱�Ƃł���B ���̉e���͒������b�V�����O�p��l�ʑ̂ȂǁA���̍\���𗘗p���邩�A �⊮�@��p���邱�Ƃɂ���Čy�������B