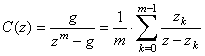
���̏͂ł̓t�B�[�h�o�b�N�E�f�B���C�E�l�b�g���[�N�̉�͂������B 3.1�߂�2.5�߂ŏЉ�����j�b�g�E�R���t�B���^�̓����ɂ��ĊT������B 3.2�߂ł͕���R���t�B���^�E�l�b�g���[�N�̓�����ΏۂƂ��A ���̐v�ł����Ɏ��g���ˑ��̃��o�[�u�E�^�C���邩���������B 3.3�߂ɂ����Ă͕���R���t�B���^�E�l�b�g���[�N�Ɋ�Â��Ĉ�ʓI�� �t�B�[�h�o�b�N�E�f�B���C�E�l�b�g���[�N���o���B
Fig. 2.5�̃��j�b�g�E�R���t�B���^�̓`�B����( 2.10 )�ɂ���ė^�����A ���̂悤�ɍĐ������邱�Ƃ��ł���B
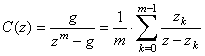
��L�̕������ɂ����āA��zk�i0 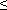 k
k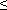 m-1�j
��
m-1�j
��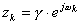 �ɂ���Ē�`����A������
�ɂ���Ē�`����A������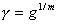 ����
����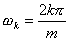 �ł���B
����Fig. 2.6c�Ō����悤�ɁA�ɂ͓����������������A�P�ʉ~�̎��͂Ɉʒu����B
�t�B�[�h�o�b�N������1�ȉ��ł���AFig. 2.6d�ɐ}�������悤�ɁA
�Ƀp�^�[���͓��ʂ̎w�����I�Ɍ������鐳���Ȑ��ɑ�������B
( 3.1 )�̋t�ϊ��͈ȉ��̃t�B���^�̃C���p���X������^����B
�ł���B
����Fig. 2.6c�Ō����悤�ɁA�ɂ͓����������������A�P�ʉ~�̎��͂Ɉʒu����B
�t�B�[�h�o�b�N������1�ȉ��ł���AFig. 2.6d�ɐ}�������悤�ɁA
�Ƀp�^�[���͓��ʂ̎w�����I�Ɍ������鐳���Ȑ��ɑ�������B
( 3.1 )�̋t�ϊ��͈ȉ��̃t�B���^�̃C���p���X������^����B
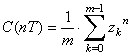 (n
(n 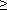 0)
0)
N�̃��j�b�g�E�R���t�B���^�����ɑg�ݍ��킹��ƁA ���̃V�X�e���̓`�B���͎��̂悤�ɂȂ�B
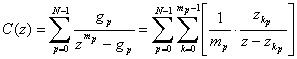
�u�s�����ȁv�f�B���C��mp��I�����邱�ƂŁA
���j�b�g�E�R���t�B���^�̑S�Ă̌ŗL���[�h�i���g���s�[�N�j�͕ʌƂȂ�B
�i = 0 �����
= 0 �����  =
=  �̏ꍇ�������j
���U������g���s�[�N�̑����́A�T���v�����ŕ\���ꂽ
�S�Ẵ��j�b�g�E�R���t�B���^�̃f�B���C���̍��v�̔����ɓ������B
�̏ꍇ�������j
���U������g���s�[�N�̑����́A�T���v�����ŕ\���ꂽ
�S�Ẵ��j�b�g�E�R���t�B���^�̃f�B���C���̍��v�̔����ɓ������B
Jot��Chaigne [16]���w�E�����悤�ɁA�ɂ̓������������Ȃ��Ƃ��Ă��A �������̋��U������g�������o���邱�ƂɂȂ�B ����͊e�R���t�B���^�̌������Ԃ��قȂ邩��ł���B �����ω����őS�ẴR���t�B���^�̌��������ɂ́A �S�Ă̋ɂ̓������������Ȃ���Ȃ�Ȃ��B ����䂦�ɁA���̌����ɏ]��˂Ȃ�Ȃ��B
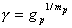 �i������p�ɂ��āj
�i������p�ɂ��āj
����̓t�B�[�h�o�b�N����gp�����S�ẴR���t�B���^p �̒���mp�ɊW����B Fig. 3.1�͕���R���t�B���^�̃C���p���X�����̊��炩�Ȍ����������Ă���B�i��l�ȋɓ��������Ƃ��j
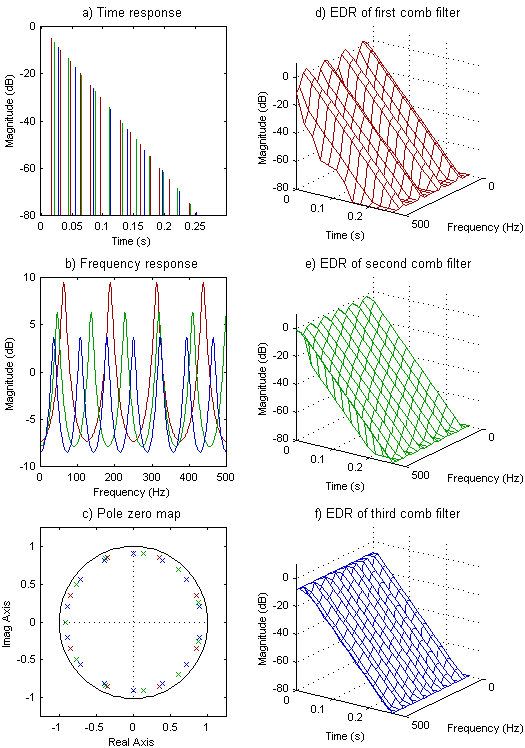
����( 3.4 )�����炷�邱�ƂŃR���t�B���^����l�Ȍ������Ԃ������Ƃ͊m���ɂȂ�B �������Ȃ���A��蒷���f�B���C�� mp�����R���t�B���^�́A ( 3.3 )�Ɍ�����悤�Ȃ��ア�����̎��g���s�[�N�i�ŗL���[�h�Ƃ��Ă��j����肾���B ���̉e�������炷���߁A�Z���f�B���C���ƒ����f�B���C���̕����ł��邩���菬�������悤�Ƃ��邱�Ƃ��ł���B ����Ȃ킯��Schroeder [39]�̓R���t�B���^�̃f�B���C���̊Ԃ̍L������ő�1:1.5�ƒ�Ă����̂ł���B ���̖����������ʂ̕��@�́A�o�͂����v����O�Ɋe�t�B���^�̗��������̃f�B���C���ɔ�Ⴕ�ďd�ݕt���邱�Ƃł���B ����͑S�ẴR���t�B���^�̉�������l�ɕ������邱�Ƃ��m���ɂ���B ���ʂƂ��Đ�������g��������Fig. 3.2�Ɏ����B
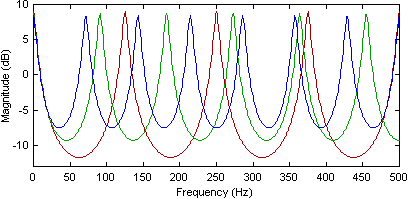
���g�����x�̓w���c���̕����肪�m�o�ł�����g���s�[�N�̐��Ƃ��Ē�`�����B �����͂��̒m�o�ł�����g�����x��2.4�߂ŋc�_�������_��̃��[�h���x�̊Ԃɍ���˂Ȃ�Ȃ��B �Ⴆ�A������Œ�Ă����悤�ȃR���t�B���^�̏o�͂����邽�߂̂����炩�̏d�ݕt���𗘗p���Ȃ��Ȃ�A �ア���g���s�[�N���m�o����Ȃ����߂Ɏ��g�����x�̓��[�h���x���Ⴍ�Ȃ邩������Ȃ��B
��2�͂ŋc�_�����悤�ɁA�ꎞ�I�ȓ��͂Ə�����Ԃ̓��͗����ɂ��ĕs�\���Ȏ��g�����x�̌��ʂɕ�������B �ꎞ�I�ȉ��ɂ��ẮA���o�[�u�̌㕔�Ɂu������v����̃��[�h��2�̃��[�h�̌ۓ������o���B �قڒ���Ԃ̓��͂ɂ��ẮA���̑��̎��g������������A������g���������グ����B �ǂ������镔�����V�~�����[�V�������邽�߂ɕK�v�Ȏ��g�����x�����肷�邽�߂ɂ́A 2.4�߂ŗp�����Ă������Q�Ƃ���Ƃ悢�B ���K�͂̃z�[���i18100 m3�ART1.8�b�j��fc = 20 Hz��� 2.2 Hz��̍ő���g���s�[�N���������ł��낤���Ƃ�������B ����̓w���c����0.45���[�h�̎��g�����x�ɑ�������B
���Ԗ��x�͕����肪1�b�Ԃɒm�o����G�R�[�̐��Ƃ��Ē�`�����B ���g�����x�����[�h���x�̑���Ɠ��l�ɁA ���Ԗ��x���G�R�[���x�̑���ɒ��ӂ��˂Ȃ�Ȃ��B ���ۂ̕����ɑ��݂���G�R�[���x�͂����Βm�o����鎞�Ԗ��x���傫���B ����́A���ۂ̕����Ŕ�������A���I�ȃG�R�[���ʗ�i�Ⴂ�ȗ����������A ��苭���G�R�[���ア�G�R�[���B���Ă��܂����߂ł���B ����R���t�B���^�v�̏ꍇ�A���̃G�R�[���������邽�߁A�G�R�[���x�͎��Ԗ��x�ɓ������B
�����R���t�B���^�̃f�B���C�������ׂċ����͈͓��ɂ���Ȃ�A �����ɂ���Ď��g�����x�Ǝ��Ԗ��x���T�Z���邱�Ƃ��ł���B
���g�����x: 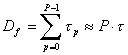
���Ԗ��x: 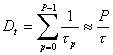
������ �̓R���t�B���^�̕��σf�B���C���is�j�A
N�̓R���t�B���^�̐��ł���B
�]���āA���g�����x�Ǝ��Ԗ��x���^������A�����̃R���t�B���^���g���ׂ����A
���σf�B���C�������ł��邩��������p���ċ��߂邱�Ƃ��ł���B
�̓R���t�B���^�̕��σf�B���C���is�j�A
N�̓R���t�B���^�̐��ł���B
�]���āA���g�����x�Ǝ��Ԗ��x���^������A�����̃R���t�B���^���g���ׂ����A
���σf�B���C�������ł��邩��������p���ċ��߂邱�Ƃ��ł���B
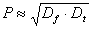 �����
����� 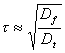
�Ⴆ�A���Ԗ��xDt = 1000�iSchroeder [39]�ɂ���Ē�Ă��ꂽ�悤�Ɂj�A ���g�����xDf = 0.45���������悤�Ƃ���A 21�̃R���t�B���^��21 ms�̕��σf�B���C��v���邱�ƂɂȂ邾�낤�B Griesinger�͍L�ш敝�̃��o�[�u�E���j�b�g�͖��b10,000���z����قǂ� �������Ԗ��x�����ׂ��ł���ƒ�Ă����B ����ɂ͂Ȃ��67�ȏ���̃R���t�B���^��v���邱�ƂɂȂ�B �K���ɂ��A3.3�߂Ō���悤�Ƀt�B�[�h�o�b�N�E�f�B���C�E�l�b�g���[�N�� ���̖����������邱�ƂɂȂ邾�낤�B
��2�͂ŁA���o�[�u�E�^�C����60 dB�܂Ō�������̂ɂ����鎞�ԂƂ��Ē�`���ꂽ�B ���������̕���R���t�B���^�ɂ��āA���ׂẴR���t�B���^�E���j�b�g�͓������x�Ō�������B �����ɂ��A�����̌������x��dB / �T���v�������Ƃ��ċ��߂邱�Ƃ��ł���B
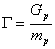 �i���ׂĂ�p�ɂ��āj
�i���ׂĂ�p�ɂ��āj
���̎���( 3.4 )�̂��̂Ɠ��������A�����ł�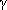 ��gp�̑���ɁA
dB�ŕ\���ꂽ
��gp�̑���ɁA
dB�ŕ\���ꂽ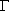 ��Gp��p����B
�i
��Gp��p����B
�i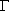 = 20 log(
= 20 log(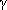 ) �A Gp = 20 log(gp)�j
Schroeder�ɂ�郊�o�[�u�E�^�C���̒�`��( 3.8 )��p���邱�ƂŁA
���ꂼ��̃R���t�B���^�̃��o�[�u�E�^�C�������߂邱�Ƃ��ł���B
) �A Gp = 20 log(gp)�j
Schroeder�ɂ�郊�o�[�u�E�^�C���̒�`��( 3.8 )��p���邱�ƂŁA
���ꂼ��̃R���t�B���^�̃��o�[�u�E�^�C�������߂邱�Ƃ��ł���B
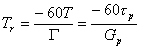
������Tr�̓��o�[�u�E�^�C���AT�̓T���v�����O�����A
������ p = mp
p = mp T�ł���B
�R���t�B���^�̃f�B���C�����t�B�[�h�o�b�N������ύX���邱�ƂŁA���o�[�u�E�^�C����ς��邱�Ƃ��ł���B
�f�B���C���̑����ւ̕����I�ȗގ��́A���z�I�ȕ����̃T�C�Y�̑����ƂȂ邾�낤�B
�����A�t�B�[�h�o�b�N�����̌����͋�C���ł̉����`�d���ɋN����z���̑��ʂƂ��čl������B
�������Ȃ���A�ǂɂ��z���̑��ʂ��ω����錴���ƂȂ邽�߁A
����痘����ύX����ۂɂ͒��ӂ��ׂ��ł���B
�i����͕����̃T�C�Y������ύX���悤�Ǝ��݂�Ƃ��ɕύX���ׂ��ł͂Ȃ��j
�f�B���C����
T�ł���B
�R���t�B���^�̃f�B���C�����t�B�[�h�o�b�N������ύX���邱�ƂŁA���o�[�u�E�^�C����ς��邱�Ƃ��ł���B
�f�B���C���̑����ւ̕����I�ȗގ��́A���z�I�ȕ����̃T�C�Y�̑����ƂȂ邾�낤�B
�����A�t�B�[�h�o�b�N�����̌����͋�C���ł̉����`�d���ɋN����z���̑��ʂƂ��čl������B
�������Ȃ���A�ǂɂ��z���̑��ʂ��ω����錴���ƂȂ邽�߁A
����痘����ύX����ۂɂ͒��ӂ��ׂ��ł���B
�i����͕����̃T�C�Y������ύX���悤�Ǝ��݂�Ƃ��ɕύX���ׂ��ł͂Ȃ��j
�f�B���C���� ���|���邩�A
�t�B�[�h�o�b�N�����idB�j��
���|���邩�A
�t�B�[�h�o�b�N�����idB�j�� �Ŋ��邱�ƂŁA
���o�[�u��
�Ŋ��邱�ƂŁA
���o�[�u�� �������邾�낤�B
������ɂ��Ă����ڂ��ׂ��́A�V�X�e���̎��Ԗ��x�Ǝ��g�����x���ύX�����Ƃ������Ƃł���B
�������邾�낤�B
������ɂ��Ă����ڂ��ׂ��́A�V�X�e���̎��Ԗ��x�Ǝ��g�����x���ύX�����Ƃ������Ƃł���B
Schroeder [39]�ɂ���Ē�Ă�����Moorer [27]�����������悤�ɁA �R���t�B���^�̃t�B�[�h�o�b�N�E���[�v�Ƀ��[�p�X�t�B���^���������ނ��Ƃ́A �����炩�̎��g���]���̌������x���B �ǂ�����g���������g���z������X�������邽�߁A ����͕ǂ̋z�����V�~�����[�g���邽�߂ɗ��p�����B
�t�B�[�h�o�b�N����gp��`�B��hp(z)�����t�B���^�ɍ����ւ���ƁA ���g���]���̃��o�[�u�E�^�C���邱�Ƃ��ł���B ���o�[�u�ɂ���Ď������܂��s���R�Ȓ��F���m���ɔ��������̂Ȃ�A �����z���t�B���^���������ނƂ��ɂ͒��ӂ��ׂ��ł���B ���ׂẴR���t�B���^���������Γx���̋z���������Č������������Ƃ���ł���B ����́AJot ����� Chaigne [16]��z���ʂɂ������ɂ̋O�Ղ̘A�����ƌĂ� ���̏��������炷�邱�ƂŒB���ł���B
�E�E�E������\���Ɍ���ꂽ���g���ш�i���o�[�u�E�^�C����萔�Ƃ݂Ȃ��Ă悢�قǂ́j�ɂ����āA ���ׂĂ̌ŗL���[�h�͓���̌������Ԃ����͂��ł���B ���l�ɁA�אڂ���ŗL�U�����ɑΉ�����V�X�e���ɂ͓���̓��������͂��ł���B
���ׂẴR���t�B���^�͕s���R�ȃ��o�[�u������邽�߂ɂ��̏��������炷�ׂ��ł���B
�����`�B��hp(z)���P�Ɏ��g���]���̗���gp =
| hp(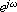 ) |�ł���A
�ɂ̋O�Ղ̘A�����͕�����( 3.4 )���瓾����( 3.10 )�ɂ���ĕۏ����B
) |�ł���A
�ɂ̋O�Ղ̘A�����͕�����( 3.4 )���瓾����( 3.10 )�ɂ���ĕۏ����B
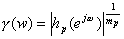 �i���ׂĂ�p�ɂ��āj
�i���ׂĂ�p�ɂ��āj
���̃��o�[�u�E�^�C���͂܂����g���]���ł���A�����ɂ���ė^������B
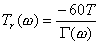 0
0 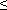

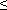

Fig. 3.3���ɂ̋O�Ղ̘A���������ɏ]�����g���]���̌�������
�iTr(0) = 3 s ����� Tr( ) = 0.15 s�j
��������R���t�B���^����������B
) = 0.15 s�j
��������R���t�B���^����������B
�Ō�ɁA�P�ʉ~���ɂ����邢�����A���邢�͂��ׂẴR���t�B���^�̋����ɂ̈ʒu��ύX�����
�ŗL���[�h�̈ꕔ������荂���G�l���M�[�����悤�ɂȂ邱�Ƃɗ��ӂ��ׂ��ł���B
����́AFig. 3.3b�Ɍ�����悤�ɏo�͂̑S�̓I�Ȏ��g��������ς���B
�������Ȃ���A�`�B��t(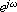 )������
���̂悤�ȒP���ȉ�����t�B���^��lj�����i����R���t�B���^�ƒ���ڑ�����j���ƂŁA
)������
���̂悤�ȒP���ȉ�����t�B���^��lj�����i����R���t�B���^�ƒ���ڑ�����j���ƂŁA
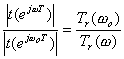
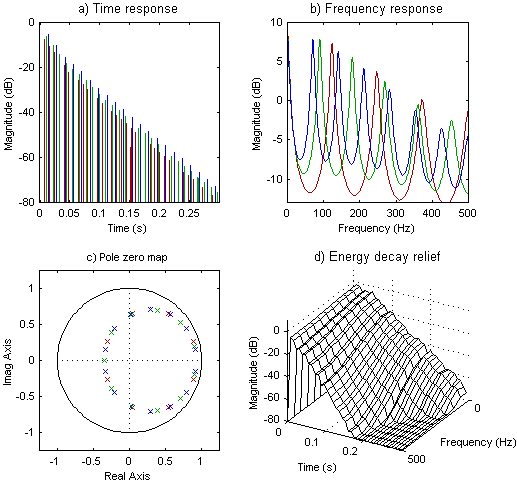
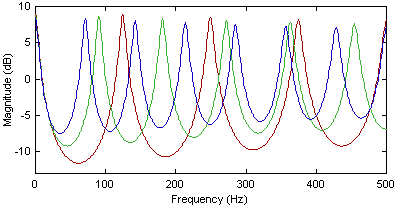
Fig. 3.4�Ɏ����悤�Ȏ��g���ŗL�̃��o�[�u�E�^�C���Ɩ��W�ȑS�̂̎��g��������������B
Jot�͋z�����������邽�߂Ɉꎟ�̖����C���p���X�����iIIR�j�t�B���^���g�����Ƃ��Ă��A ���������p�̈ꎟ�̗L���C���p���X�����iFIR�j�t�B���^�Ƒg�ݍ��킹���B �v�ŗp������ł��낤�z���t�B���^�͈ȉ��̓`�B�������B
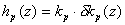 ������
������ 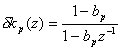
������ 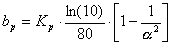 �ł���A�܂�
�ł���A�܂�
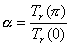 �ł���B
�ނ����p��������ɑ������鉹����t�B���^�͈ȉ��̓`�B��������FIR�t�B���^�ł������B
�ł���B
�ނ����p��������ɑ������鉹����t�B���^�͈ȉ��̓`�B��������FIR�t�B���^�ł������B
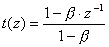
������ 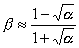 �ł���B
�o���̃t�B���^�𗘗p���Č��ʓI�ɓ�����V�O�i���E�t���[��Fig. 3.5�Ɏ����B
�ł���B
�o���̃t�B���^�𗘗p���Č��ʓI�ɓ�����V�O�i���E�t���[��Fig. 3.5�Ɏ����B
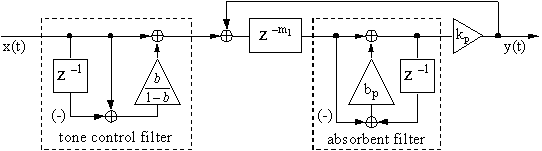
�O�߂Ō����悤�ɁA�K���Ȏ��g�����x���^����ꂽ����R���t�B���^�v�ɂ����� �\���Ȏ��Ԗ��x�邽�߂ɂ͔��ɑ����̃R���t�B���^���K�v�ƂȂ�B ���傫�Ȏ��Ԗ��x�邽�߂̃t�B���^�v�ɂ��ẮA��2�͂ł������q�ׂ��B �����v�̈ꕔ�A�Ⴆ�Β���I�[���p�X�t�B���^�́A�₪�Ď��ۂ̕����Ŋϑ������悤�� �G�R�[���x�̑��������������B ���z�I�ɂ́A����R���t�B���^�ƒ���I�[���p�X�t�B���^�o���̓������������̂Ɉ�ʓI�ɏ\���� �B��̃l�b�g���[�N�����o�������Ƃ���ł���B �܂��A����R���t�B���^�ō�邱�Ƃ̂ł��铯��̎��g���]�������������������B ���̐��ł͂��̖ڕW�ɓ��B���邽�߂Ɏ����@�ɂ��ďq�ׂ�B
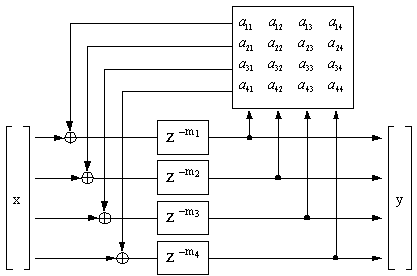
Gerzon [11]�͏��߂ĒP��̃}���`�`�����l���E�l�b�g���[�N�̊T�O����ʉ����A ����͊�{�I�Ƀ��j�b�g�E�I�[���p�X�t�B���^�Ɠ�����N�����̂��̂ł������B �Ԃ��Ȃ�Stautner�����Puckette [47]��N�̃f�B���C���C���ƃt�B�[�h�o�b�N�s��A �Ɋ�Â���ʓI�ȃl�b�g���[�N���Ă����B�����Fig. 3.6�Ɏ����B ���̍s��ɂ����āA�e�W��amn�̓f�B���C���C��n����o�Ă��� �f�B���C���C��m�̓��͂ɑ�����M���̗ʂɑ�������B ���̃V�X�e���̈��萫�̓t�B�[�h�o�b�N�s��A�Ɉˑ�����B ���҂�A�����j�^���s���|g| < 1�̗����W��g�̐ςł���Ƃ��� ���萫���m���ɂȂ邱�Ƃ������B ���̃V�X�e���̂��̑��̓����Ƃ��ẮA�o�͂����݂ɔł��邽�߂� �}���`�`�����l���E�V�X�e���ɂ����Ă͕ʓr�̏�����v�������p�ł��邱�Ƃ���������B
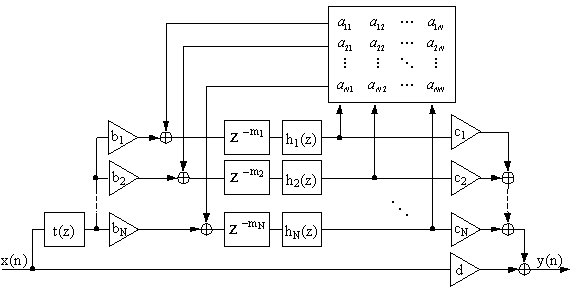
Jot�����Chaigne�́AFig. 3.7�Ɏ������V�X�e���𗘗p���� ���̐v����肢��������ʉ������B �x�N�g���\�L�@��Z�ϊ���p����Ƃ��A���̃V�X�e���̕������͈ȉ��̂悤�ɂȂ�B
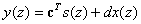
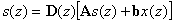
�����ŁA
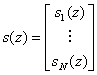
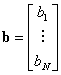
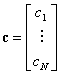
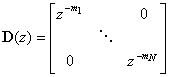
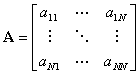
�}���`���́A�}���`�o�͂̃V�X�e���Ɋւ��āA �x�N�g��b��c�͍s��ƂȂ�B ������( 3.17 )�����( 3.18 )��s(z)����������ƁA �ȉ��̃V�X�e���`�B�����������B
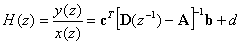
�V�X�e���̃[���s��͎����ɂ���ė^������B
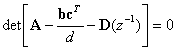
�]���āA���̃V�X�e���̋ɂ͎��̓����������̉��ł���B
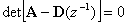
���̕������̕��͓I�ȉ��͎����ł͂Ȃ��B �������Ȃ���A����̃t�B�[�h�o�b�N�s��ɂ��Ă��̕������������̂͗e�Ղł���B
Jot�����Chaigne�́A�K�ȍs���p���邱�ƂŃ��j�b�g�E�t�B���^�i�R���ł��I�[���p�X�ł��j �̂�����g�ݍ��킹��\�����邱�Ƃ��w�E�����B �Ⴆ��A���Ίp�s��ł���Ƃ��A�V�X�e����3.2�߂ŏq�ׂ�����R���t�B���^��\���B �܂��A�O�p�s�����������Ă����B�Ȃ��Ȃ炻�̏ꍇ�A������( 3.21 )�͈ȉ��̂悤�ɕό`����邩��ł���B
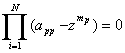
����I�[���p�X�t�B���^�͂��ꎩ�g���O�p�t�B�[�h�o�b�N�s�� �i�t�B�[�h�o�b�N����gp�ɓ������Ίp�����������j�̃l�b�g���[�N�ł���B �]���āA����R���t�B���^�Ɠ����f�B���C���ƃt�B�[�h�o�b�N������������I�[���p�X�t�B���^�͂܂��A ����R���t�B���^�Ɠ����ŗL���[�h�i���U���g���ƌ������x�j�����B
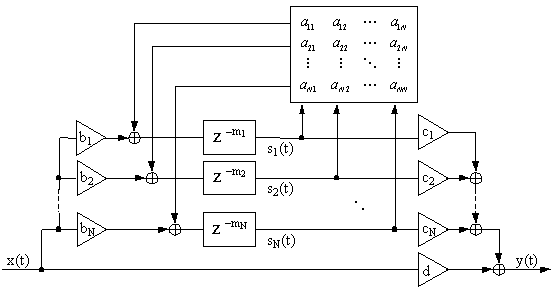
�V�X�e���̈��萫���ۏ����i���j�^���E�t�B�[�h�o�b�N�E���[�v�̋ɂ��S�ĒP�ʉ~���ɂ��邽�߁j���Ƃ���A ���j�^���E�t�B�[�h�o�b�N�s��͍ł������p�����Ă����B �����̍s��̓l�b�g���[�N���ׂĂ��ɏ��邱�Ƃœ��͐M���̃G�l���M�[��ێ�����B ����āA���j�^���E�t�B�[�h�o�b�N�s��͏���t��FDN�v���g�^�C�v�����o���B �Ƃ͂������̑��̎�ނ̃t�B�[�h�o�b�N�s����܂����ʓI�ɉt�V�X�e���ƂȂ蓾��B
�l�b�g���[�N�̌������Ԃ𐧌䂷�ׂ��AJot��Chaigne�͂��ꂼ��̃f�B���C���C���̌�� ���܂��z���t�B���^��g�ݍ��킹���t�t�B�[�h�o�b�N�s���p���邱�Ƃ��Ă����B �R���t�B���^���ׂĂ����x�Ō��������A�ɂ̋O�Ղ̘A�������d�邽�߂ɂ́A �ȉ��̕����������炳��Ȃ���Ȃ�Ȃ��B
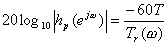
����͑����A�ɂ�P�ʉ~���烊�o�[�u�E�^�C��Tr�ɂ���Ē�`�����Ȑ��Ɉړ������邾�낤�B ����ɁA�����3.2.4�߂ŏq�ׂ�������t�B���^�̗��p�ɂ���Ē������꓾�� �S�̓I�ȍ����g�̌��������ƂɂȂ邾�낤�B �z���t�B���^�Ɖ�����t�B���^���܂ލŏI�I��FDN��Fig. 3.8�Ɏ����B
�t�B�[�h�o�b�N�s��̑I��́A�S�̓I�ȉ��ƃ��o�[�u���[�^�̌v�Z�v���Ɋւ��ċɂ߂ďd��ł���B 3.3.1�߂ŋc�_�����悤�ɁA����R���t�B���^�l�b�g���[�N�ɑ�������Ίp�s��Ȃǂ��Ƃ��āA �����̍s�t�v���g�^�C�v�����o���B �Ⴆ�AStautner�����Puckette [47]�͈ȉ��̍s���p�����B
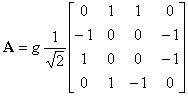
������|g| = 1�̏ꍇ�AA�͉t�ł���B ����́A�}���`�`�����l���o�̓V�X�e���ŗ��p�����Ƃ��̂��̋����[�������ɂ����̂ł���B �������A�d��ȉ��P��0�̌W���������Ȃ����j�^���s��𗘗p���邱�Ƃœ�����B ����͓��ʂ̃f�B���C���C����K�v�Ƃ��邪�A�ő�̖��x�����o�����낤�B
�����������s��̂ЂƂ̓n�E�X�z���_�[�s�� [17]�̗ނ���I��A���̂悤�Ɍ��ʓI�Ɏ��������B
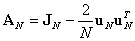
������JN��N x N�̏���s��ł���A
uN�͂���N x 1�̗�x�N�g���ł���B
���ʂƂ��ē�����s��͓�̈قȂ��[���l���܂ނ��߁A�G�R�[���x���ő剻����B
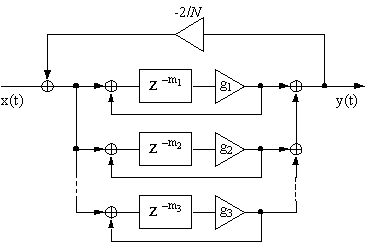
�܂��AA N · x(z)��
JN�ɏ]����x(z)�̗v�f����בւ��A
���͂̐����ɗv�f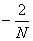 ���|�������̂̍��v�����Z���邱�Ƃɂ���Č����I�Ɍv�Z�ł���B
�����N x N�̍s��̏�Z�ɂ͒ʏ�N2��̉��Z��
�v����̂ɔ�ׁA���悻2N��̉��Z�ōςނ��ƂɂȂ�B
JN���P�ʍs�� IN�ł���Ƃ������ʂȏꍇ�ɂ́A
���ʂƂ��ē�����V�X�e����Fig. 3.9�Ɏ����悤�ȍő�̃G�R�[���x��������R���t�B���^�̂悤�ɐU�镑���B
Jot�́A���̃V�X�e�����S�f�B���C���̍��v�ɑ������鎞�ԊԊu���Ɏ����I�ȃN���b�N���ݏo�����ƂɋC�Â����B
�������Ȃ���A���̑S�Ă̌W�� cN�̕����]�����邱�ƂŁB
�V�X�e���̏o�͂ł͂����̃N���b�N����������邱�Ƃ��ł���B
���|�������̂̍��v�����Z���邱�Ƃɂ���Č����I�Ɍv�Z�ł���B
�����N x N�̍s��̏�Z�ɂ͒ʏ�N2��̉��Z��
�v����̂ɔ�ׁA���悻2N��̉��Z�ōςނ��ƂɂȂ�B
JN���P�ʍs�� IN�ł���Ƃ������ʂȏꍇ�ɂ́A
���ʂƂ��ē�����V�X�e����Fig. 3.9�Ɏ����悤�ȍő�̃G�R�[���x��������R���t�B���^�̂悤�ɐU�镑���B
Jot�́A���̃V�X�e�����S�f�B���C���̍��v�ɑ������鎞�ԊԊu���Ɏ����I�ȃN���b�N���ݏo�����ƂɋC�Â����B
�������Ȃ���A���̑S�Ă̌W�� cN�̕����]�����邱�ƂŁB
�V�X�e���̏o�͂ł͂����̃N���b�N����������邱�Ƃ��ł���B
�~����s��ɂȂ�悤��JN��I�Ԃ��Ƃ́A������̋����[���\���ł���B �Ȃ��Ȃ炱�̍\���ɂ����Ă̓f�B���C���C�������݂ɒ���ɑ��荞�܂�邩��ł���B ����̓V�X�e���̍ŏI�I�Ȏ����ɂ����郁�����Ǘ���e�Ղɂ���B
�܂��ARocchesso�����Smith [31]�͈ȉ��̂悤�Ȍ`������� ���j�^���z�t�B�[�h�o�b�N�s��̗��p���Ă����B
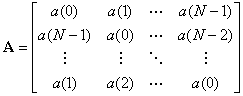
�ȉ��̏z�s���Ίp�s��ɂ��邽�߁A���U�t�[���G�ϊ��iDFT�j�s��T���g�����Ƃ��ł���B
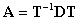
����́A��1���DFT�����߂邱�Ƃɂ��A�̌ŗL�l���Z��ł��邱�Ƃ������B
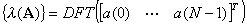
������{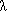 (A)}��A
�iD�̑Ίp�������j�̌ŗL�l�ł���B
�����̌ŗL�l���P�ʌW�������Ƃ��A�z�s��͉t�ƂȂ邾�낤�B
�z�t�B�[�h�o�b�N�s��𗘗p���邱�Ƃɂ͎�ȗ��_�������B
�ЂƂ͋�̓I�ȌŗL�l���V�X�e���̐v���ɓ���ł��邱�ƁA
������͍����t�[���G�ϊ����g���邽�߁A�s��̏�Z���v�Z����̂ɖ�N log(N)
��̉��Z�����K�v�Ȃ����Ƃł���B
(A)}��A
�iD�̑Ίp�������j�̌ŗL�l�ł���B
�����̌ŗL�l���P�ʌW�������Ƃ��A�z�s��͉t�ƂȂ邾�낤�B
�z�t�B�[�h�o�b�N�s��𗘗p���邱�Ƃɂ͎�ȗ��_�������B
�ЂƂ͋�̓I�ȌŗL�l���V�X�e���̐v���ɓ���ł��邱�ƁA
������͍����t�[���G�ϊ����g���邽�߁A�s��̏�Z���v�Z����̂ɖ�N log(N)
��̉��Z�����K�v�Ȃ����Ƃł���B
Fig. 3.10��N����FDN�ɑ�������\���� N����̃f�W�^�����g�H�l�b�g���[�N�iDWN�j��\���Ă���B ���̍\���ɂ����邻�ꂼ��̎}��FDN�̃f�B���C���C����\���A ���ꂼ��̓��g�H�̒����͑Ή�����f�B���C���C���̒����̔����ł���B ����͐i�s�g�������̐ړ_����}�̏I�[�ɐi�݁A���ꂩ�璆���̐ړ_�ɖ߂��Ă���͂�������ł���B ��̃f�B���C���C���͒P��̃f�B���C�f�q�ō\������锽�ˏI�[�������������̓��g�H�ɕϊ��ł���B
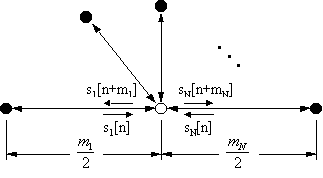
pi+ = si(n) �����pi¯ = si(n+mi) ���`����ƁA���ʂ�DWN�̕\�L��������B
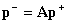
������p+��n���_�ɐړ_�ɓ��B���� �����Ă���i�s�g�T���v���̃x�N�g���iFDN�ł̓f�B���C���C���̏o�́j�A p¯��n���_�ɐړ_�𗣂��o�Ă����i�s�g�T���v�� �iFDN�ł̓f�B���C���C���̓��́j�A������A�͓��g�ǂ̐ړ_�ƌ��т��� ���U�s���iFDN�ł̓t�B�[�h�o�b�N�s��j�ł���B
Rocchesso�����Smith [31]�͐ړ_�ɂ����镡�f�͂̍��v�����U�����s�ςł���Ƃ��A ���̕��U�s��͉t�ƂȂ�Ƃ����邱�Ƃ��������B���Ȃ킿�A
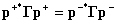

������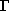 �̓G���~�[�g�ł���A
�ėp�̐ړ_�̃A�h�~�^���X�Ƃ��Đ�������鐳��l�s��ł���B
Fig. 3.10�̏ꍇ�A���ꂼ��̓��g�H�͓����I�ȃA�h�~�^���X
�̓G���~�[�g�ł���A
�ėp�̐ړ_�̃A�h�~�^���X�Ƃ��Đ�������鐳��l�s��ł���B
Fig. 3.10�̏ꍇ�A���ꂼ��̓��g�H�͓����I�ȃA�h�~�^���X
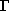 i��
�s��
i��
�s��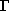 = diag(
= diag(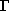 1,
1,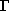 2,
�,
2,
�, 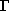 N)�����B
���̏ꍇ�AA�̓��j�^���A
N)�����B
���̏ꍇ�AA�̓��j�^���A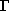 = I�ł���B
�]���āA���ꂼ��̓����I�ȃA�h�~�^���X?i��1��DWN�̓��j�^���E�t�B�[�h�o�b�N�s�������FDN�ɑ�������B
���ꂼ��̓��g�H��1���قȂ�����I�ȃA�h�~�^���X������������Ȃ����Ƃ���A
DWN������ʓI�ȗނ̉t���U�s������Ƃ�������B
�������Ȃ���A�S�Ẳt���U�s��N���̓��g�H�̕����ړ_�Ƃ��Đ����ł���킯�ł͂Ȃ��B�i�Ⴆ�Ώ���s��Ȃǁj
= I�ł���B
�]���āA���ꂼ��̓����I�ȃA�h�~�^���X?i��1��DWN�̓��j�^���E�t�B�[�h�o�b�N�s�������FDN�ɑ�������B
���ꂼ��̓��g�H��1���قȂ�����I�ȃA�h�~�^���X������������Ȃ����Ƃ���A
DWN������ʓI�ȗނ̉t���U�s������Ƃ�������B
�������Ȃ���A�S�Ẳt���U�s��N���̓��g�H�̕����ړ_�Ƃ��Đ����ł���킯�ł͂Ȃ��B�i�Ⴆ�Ώ���s��Ȃǁj