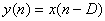
リバーブの音を向上させるための一般的なFDNアルゴリズムのため、 また、そうしないと動きがないリバーブに活気を加えるために何種類かの可変化改造をすることができる。 例えば、FDNのフィードバック行列をリアルタイムに変えれば、 時間とともに音色が変わるリバーブレータが作り出されるだろう。 また、出力行列(Fig. 3.7では係数cN)を変えることもできる。 この論文ではFDNのディレイ長をリアルタイムに変更するための変調の利用について研究する。 これらのディレイ長を変えることで、共振周波数を絶えず変化させ、 それによってより平らに知覚される周波数応答を持つリバーブを達成するのである。
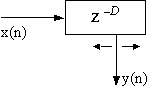
Fig. 4.1およびFig. 4.2は典型的な変調されたディレイラインを示している。 ここで、ディレイラインの出力位置は中心位置の周辺を絶えず移動する。 このディレイラインの出力は次式によって与えられる。
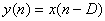
ただし 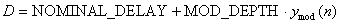
ここでNOMINAL_DELAYは変調の中心位置、 MOD_DEPTHは中心位置からそれぞれの側への変調の振幅、 ymod(n)は波形生成器の出力、 そしてDは次のように整数部分と端数部分に分けられる正の実数である。
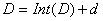
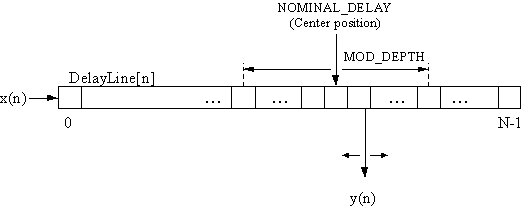
d 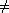 0のとき、
x(n - D)の値は2つのサンプルの間に収まり、
従って補完されるはずである。
0のとき、
x(n - D)の値は2つのサンプルの間に収まり、
従って補完されるはずである。
様々な波形形式を変調源に利用でき、 また、様々な技術をディレイラインの出力値を補完するために利用することができる。 最も興味深い変調形式と補完形式についてはそれぞれ4.1節と4.2節で紹介するつもりである。
最も一般的な変調源は単純なシヌソイド発振器である。 そのような発振器を実装する手段は数多い。 そのひとつに、係数があらかじめ計算されメモリに格納されたルックアップテーブルを用いる方法がある。 しかしながら、この論文の目的は少ないメモリしか必要としない(加えて効率的な)アルゴリズムを作り出すことであるので、 数ワードのメモリしか必要としない別の方法を選ばねばならなかった。 この実装はサイン関数のZ変換に基づいている。
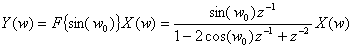
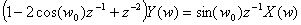
ここで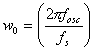 ,foscは
望まれる発振器周波数、そしてfsはサンプリングレートである。
X(w)は発振器を開始させるためのインパルス信号で、以下の時間領域に定義される。
,foscは
望まれる発振器周波数、そしてfsはサンプリングレートである。
X(w)は発振器を開始させるためのインパルス信号で、以下の時間領域に定義される。
n = 0のとき x(n) = 1
n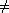 0のとき x(n) = 0
0のとき x(n) = 0
( 4.5 )の逆Z変換を取ることで以下の時間領域の方程式が得られる。
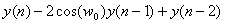
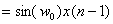 = 0 (n > 1のとき)
= 0 (n > 1のとき)
<=>
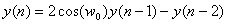 (n > 1のとき)
(n > 1のとき)
ここで初期条件は次式により与えられる。
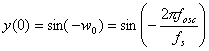
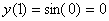
ここでfoscは望まれる発振器周波数、fsは サンプリングレートである。 このアルゴリズムが、実装プラットフォームのワード長が有限であるために、 いくつかの周波数について不安定であり得ることに留意することが大切である。 このアルゴリズムの実装についてより詳しいことは5.4.1節で示すことになるだろう。
ローパスフィルタ処理された擬似ランダム系列も変調源として利用できる。 実際には単純な一様擬似乱数ジェネレータ(RNG)で十分で、効率的に実装できる。 Knuth [23]により提案されたRNGの一種は、以下の方程式を用いる線形合同法に基づく。
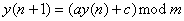
複数のRNGを同時使用しない限り、初期値あるいは種は一般的にあまり重要でない。 この場合はそれぞれについて唯一の種を選択するのが望ましい。 良いジェネレータは出力系列を繰り返す前にm個の値を生成するので 変数aとcの選択は決定的に重要であり、 0からm-1までの全ての数はジェネレータの周期毎に1度に出力されるべきである。 しかしながら複数のジェネレータを同時使用せねばらならない場合、 全ての系列が相いに異なるように見えるように、 それぞれのRNGについて異なる種を選択すべきである。 絶対値mは、「ユーザに意識させないで」mod関数を実行するために、 通常実装プラットフォームのワード長に従って選択される。 例えば、プロセッサのワード長が32bitの実装プラットフォームでは、 絶対値として32を選択することになる。 実装についてより詳しいことは5.4.2節で与えられるだろう。 用いた他のパラメータ(a = 1664525 and c = 32767) はKnuthの公式に従って選定されたものである。
生の擬似乱数列を得たらすぐに、滑らかな発振が得られるように処理すべきである。 fs/N個のサンプルすべてについて一つの擬似乱数を使うと、 遅い発振を得ることができる。ここでfsはサンプリングレート、 そしてNは実験的に定められた定数である。 それから、線形補完を利用して中間値を得るのも良いだろう。 しかしながら、発振傾斜における突然の変化はリバーブの出力に突然の音程変化を引き起こすであろうから、 この手法は今回の用途には不適当である。 より良い音がする方法(より計算が集約的であるとはいえ)としては、 中間点をゼロで埋め、結果の系列にローパスフィルタをかけることである。 元の系列をゼロで埋めると、一つの乱数をN個のサンプル全てと計算するため、 全体の処理がより効率的になる。(N = 100とすると良い結果が得られることが分かっている) いくつかのローパスフィルタを試した結果、 特定の突出した発振周波数の無い滑らかな出力を得るためには、 2 Hzのカットオフ周波数と0.5 dBの通過帯域リップルを持つ4次のチェビシェフフィルタ (双一次変換によって得られる)が必要であることが分かった。 2を種としたときの結果の信号をFig. 4.3に示す。
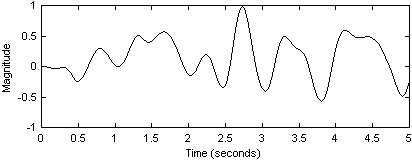
変調装置として三角波ジェネレータを利用してもあまり良い結果は得られない。 毎周期2つのはっきりした音程から成るリバーブの後部を作り出してしまうだろう。 最初の音程は上りの傾斜路に相当し、第2の音程は下りの傾斜路に相当する。 この音程の急変を避けるには、波形にローパスフィルタをかけるとよい。 しかしながら、これは余分な計算量を必要とすることになる。 従って、結果として得られる波形はシヌソイド波形に類似したものとなり、 それでいて余計な計算を必要とすることになるだろう。 計算を最小限に減らすことが目的であるわけだから、 フィルタ処理された三角波を用いる実装は見送ることになる。
もう一つの一般的な波形は鋸歯状波である。 鋸歯状波変調装置が一定の音程を持つリバーブの後部を作り出すとはいえ、 ジェネレータの周期毎にクリック音に悩まされることになる。 これは、波形の突然な転換によって引き起こされるものである。 この場合も先と同様に適切なローパスフィルタによってクリック音を取り除くことができるが、 それは計算時間の許容しがたい増加を招くことになるだろう。
可変実装において変調装置は特定のディレイラインの長さを絶えず変化させる。 例えば、最小500サンプルのディレイから、最大508サンプルのディレイという具合である。 従って、ほとんどのディレイの中間値が正確に整数となることはない。(例えば501.25など) そのためサンプルの端数のディレイが必要とされる。 変調装置の速度が遅く(数ヘルツ以下)、数サンプルの幅しかないことから、 ディレイラインにおいてディレイ長を単純に最も近い出力に四捨五入してしまうわけにはいかない。 四捨五入するだけでは可聴ノイズやクリック音がリバーブの後部に発生してしまうため、 補完を利用することが重要である。
Fig. 4.1の理想的なディレイのZ領域における伝達関数は以下の通りである。
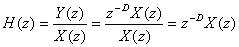
この理想的なシステムの周波数応答は次式によって与えられる。
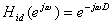
ここで = 2
= 2 ft
は正規化された周波数、Tはサンプリング周期である。
よって、H(
ft
は正規化された周波数、Tはサンプリング周期である。
よって、H(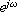 )の等級と位相応答はそれぞれ次のようになる。
)の等級と位相応答はそれぞれ次のようになる。
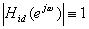 (あらゆる
(あらゆる について)
について)
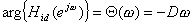
最後に、位相応答を微分し符号を反転させることでグループ・ディレイを求める。
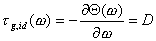
帯域制限された信号から値を補完するための端数ディレイシステムの実装は、 単一の等級と一定のグループ・ディレイDを持つ理想的な線形位相オールパスフィルタの近似値として考えられる。
そのようなフィルタのインパルス応答は逆フーリエ変換を取ることによって計算される。
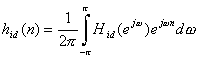 (あらゆるnについて)
(あらゆるnについて)
( 4.13 )で求まったHid(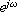 )を利用することで、
オールパスフィルタの理想的なインパルス応答が求められる。
)を利用することで、
オールパスフィルタの理想的なインパルス応答が求められる。
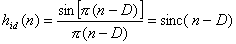 (あらゆるnについて)
(あらゆるnについて)
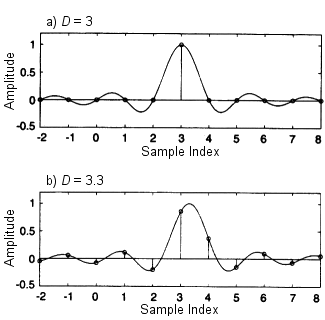
整数値のDについて、 インパルス応答はn = Dを中心とした単一のインパルスである。 他の全ての値のDについて、インパルス応答は Dを中心とするシンク関数の変化した当量に相当する。 このようなフィルタは無限長でありまた因果的でないためリアルタイムシステムにおいて 実現することは不可能である。
FIR法はすべて同一な以下のZ領域伝達関数を持つ。
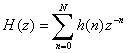
係数は周波数領域エラー関数の平均といった風に決定され、
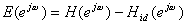
最小化される。
ラグランジュ補完の背後にある意図は特定の周波数、
一般的に o = 0
においてこのエラー関数を最大限に平坦にすることであり、
故にその近似値はこの周波数に最も近い。
これは、この時点で0に等しい周波数領域エラー関数を微分することによって得られる。
o = 0
においてこのエラー関数を最大限に平坦にすることであり、
故にその近似値はこの周波数に最も近い。
これは、この時点で0に等しい周波数領域エラー関数を微分することによって得られる。
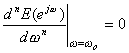 (n = 0, 1, 2, ...N)
(n = 0, 1, 2, ...N)
方程式( 4.21 )の o = 0を
微分し置換することで、L = N + 1の一次方程式一式が得られる。
これらは次式のような形式のインパルス応答として表される。
o = 0を
微分し置換することで、L = N + 1の一次方程式一式が得られる。
これらは次式のような形式のインパルス応答として表される。
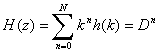 (n = 0, 1, 2, ...N)
(n = 0, 1, 2, ...N)
また、マトリックス・ノーテーション形式で、
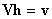
ここでhは係数を含むベクトル、VはL x Lの バンデルモンド行列である。

そしてvは、
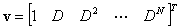
( 4.21 )の解は古典的なラグランジュ補完公式に等しく、 その係数は補完多項式に所与のデータ値一式を通らせることで得られる。 これにより次の解が導かれる。
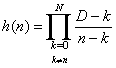 (n = 0, 1, 2, ...N)
(n = 0, 1, 2, ...N)
N = 1のとき、これは2サンプル間の線形補完に相当する。 この特定の場合、h(0) = 1 - D および h(1) = Dである。 下位のラグランジュ補完フィルタの等級と位相後退応答をFig. 4.5とFig. 4.6に示す。
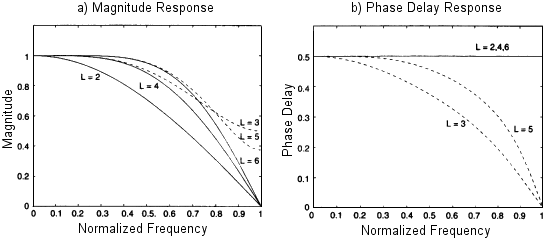
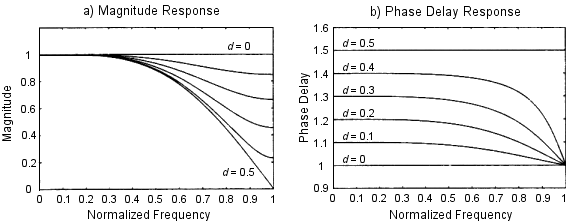
このように、偶数長のフィルタ(L= 2, 4, and 6)は線形位相である。
しかしながら、それらの振幅応答は =
=  において0に下がる。
逆に、奇数長のフィルタ(L = 3 and 5)はより良い振幅応答を持つが、
その位相後退はより悪い。
すべてのラグランジュ補完フィルタが持つ重要な特性は、
その周波数応答が決して0 dBを超えないことである。
フィードバック・ネットワークにおける安定性は確実であるべきなので、
今回の場合これは重要である。
において0に下がる。
逆に、奇数長のフィルタ(L = 3 and 5)はより良い振幅応答を持つが、
その位相後退はより悪い。
すべてのラグランジュ補完フィルタが持つ重要な特性は、
その周波数応答が決して0 dBを超えないことである。
フィードバック・ネットワークにおける安定性は確実であるべきなので、
今回の場合これは重要である。
一般的に言って、再帰的IIRフィルタはFIRフィルタに比べてよりわずかな乗算で 同等の周波数領域特性を実現することができる。 しかしながら、その設計はより複雑で、リアルタイムの係数更新中にいくつかの極が 単位円の外に出てしまったときに不安定になりうる。 N次のオールパスフィルタのZ変換関数は以下の形式からである。
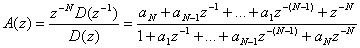
ここで分子は分母D(z)を鏡に映したものである。
最も単純なIIRフィルタ設計は0周波数における最大限に平坦なグループ・ディレイ応答を持つ 全極ローパスフィルタについてのThiranの分析的な解に基づいている。 オールパスフィルタのグループ・ディレイが全極フィルタのそれの2倍であることから、 全極Thiran公式のそれぞれのディレイ値は2倍になるべきである。 D = N + dに近づくオールパスフィルタ係数の解は次のようになる。
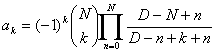 (k = 0, 1, 2, ...N)
(k = 0, 1, 2, ...N)
ここで 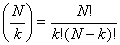 は2項係数である。[25]
係数aoは常に1に等しく、
よってこの多項式には自動的に要望どおり倍率がかけられる。
また、Thiranは十分に長いディレイDについて、
結果として得られるオールパスフィルタが常に安定であるであろうことを証明した。
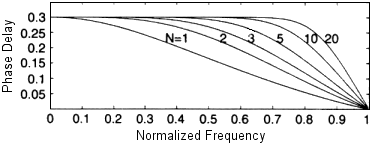
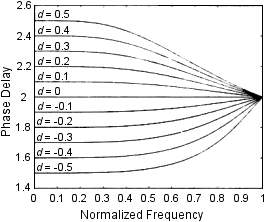
ある最大限に平坦なグループ・ディレイ設計の位相後退曲線をFig. 4.7とFig. 4.8に示す。
低次のフィルタについてさえ、遅延応答が広い周波数帯域にわたって線形であることが分かる。
は2項係数である。[25]
係数aoは常に1に等しく、
よってこの多項式には自動的に要望どおり倍率がかけられる。
また、Thiranは十分に長いディレイDについて、
結果として得られるオールパスフィルタが常に安定であるであろうことを証明した。
ある最大限に平坦なグループ・ディレイ設計の位相後退曲線をFig. 4.7とFig. 4.8に示す。
低次のフィルタについてさえ、遅延応答が広い周波数帯域にわたって線形であることが分かる。
また、Dattorro [4]は方程式( 4.28 )が次のように近似できることを提案した。
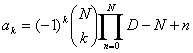 (k = 0, 1, 2, ...N)
(k = 0, 1, 2, ...N)
ここで  である。
この近似はフィルタの位相ひずみを増加させるが、彼が言及したように、
「およそ音楽的な文脈において、発生した位相ひずみは主観的に不愉快ではない」。
これらの用途について、この近似を利用することは計算の節約につながる。
である。
この近似はフィルタの位相ひずみを増加させるが、彼が言及したように、
「およそ音楽的な文脈において、発生した位相ひずみは主観的に不愉快ではない」。
これらの用途について、この近似を利用することは計算の節約につながる。
ディレイ長の変調をリバーブ・アルゴリズムで利用するという発想は新しいものではない。 これは1975年にリリースされた最初のEMTモデル250のような 初期のハードウェア・リバーブ装置で初めて利用された。 当時はメモリが限られており、よく鳴動する部屋の固有モード密度をまねるには ディレイ長をランダム化するための変調の利用が必須であった。 今日でさえ、未だに多くのリバーブ・アプリケーションが限られたメモリと 計算資源しか持っていない。(ゲーム・プラットフォームやマルチメディア・アプリケーションなどのように) Lexicon 480LやTC Electronics M3000のようなハイエンドの商用リバーブ装置でも、 より豊かなリバーブを作り出すために変調を利用していることに留意せねばならない。 しかしながら、可変技術についての文献はほとんど見当たらないのである。
2.7.2節でDattoroのプレート・リバーブレータを説明したときに述べたように、 変調はリバーブ後部の着色を減らすために利用される。 Dattorroはタンクの中のディレイラインのいくつか(あるいはすべて)を変調するために 低周波発振器(LFO)を使うことを提案した。 彼はより良い結果を得るために線形(1次のラグランジュ)補完または同等の オールパス補完を使うことを提案した。 彼は変調を用いると共振の形成を避けられることに注目した。 それはドラムやパーカッションのような高周波を含む入力信号を使ったときに顕著であった。 しかし、彼はまたピアノなどの楽器における可聴のビブラートを避けることに配慮して 変調を用いるべきであることに留意した。
処理能力の利用可能な用途については、 それぞれのディレイラインに異なる変調速度・深度を利用することを提案した。 処理時間が限られた用途については、 タンク内の4つのディレイ長のうち2つだけを変調するために 方形にしたシヌソイド発振器を使うことを提案した。
デジタル導波路を利用した人工的なリバーブに関する彼の論文 [44]の最後に、 Julius Smithは変調の利用に関する覚え書き [45]を少しだけ収録した。 彼は主に導波路リバーブの散乱係数を変調することに重点を置いた。 (これはFDNネットワークのフィードバック行列を変調するのに等しい) しかし、彼はまたアルゴリズムのディレイ長を変えることについても議論した。 彼はこのディレイ長の変化と部屋の壁の傾向を比較した。 エネルギー変調を避けるため、彼は他のディレイラインの長さが一斉に増えるときに、 同じだけひとつのディレイラインの長さを減らすことを提案した。 リバーブ後部に知覚される音程変化を隠すことを隠しやすくなることもあるため、 最終実装においてこの方法を使うことになるだろう。
Griesingerは可変合成リバーブを通じて部屋の音響効果を改善する方法を示した。[13] 彼は、演奏中のホールから知覚されるリバーブを増加させるために、電子音響補強システムで 人工的なリバーブを用いた。 そのような補強システムに元来存在するフィードバックを減らすため、 リバーブ・アルゴリズムのディレイ長を変調したのである。
先に述べたように、彼はリバーブ後部のノイズとクリック音を避けるためには 補完が必要不可欠であることに注目した。 彼はまた、ディレイ変調が音程変化をもたらすことから、 変調源は注意して選ぶべきであることにも留意した。 例えば、RNGがすべてのディレイラインに変調器として利用された場合、 それらすべてが同時に同じ傾向で作動するであろうから、 リバーブの音程の顕著な変化を招くことになるだろう。